| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 머신러닝
- cross join
- streamlit
- pandas
- 팀프로젝트
- da
- 데이터 분석
- 히트맵
- Python
- 클러스터링
- 시각화
- 프롬프트 엔지니어링
- 데이터분석
- SQLD
- Chat GPT
- 군집화
- jd
- GA4
- 태블로
- 기초프로젝트
- 크롤링
- 서브쿼리
- 프로젝트
- lambda
- 최종 프로젝트
- SQL
- 전처리
- If
- data analyst
- 기초통계
- Today
- Total
세조목
머신러닝 기초 복습(선형 회귀)(24.05.02) 본문
실제값과 예측값의 차이 = Error
Error = ∑Error ^2
→ 제곱하는 이유 : 음수 제거
→ 데이터가 추가될 때마다 Error가 커진다는 문제가 있음
→ 해결 방법 : Error / 전체 데이터 개수

※ 편향(베타 제로) = y절편
딥러닝에서의 편향과 가중치
b = 편향 + 오차
w = 가중치
Y=wX+b
w, X, b를 알면 Y 값을 알 수 있다.
Q. 가중치는 어떻게 구하지?
A. 데이터가 충분하다면 '추정' 할 수 있음
쉽게 말해 그래프를 수도 없이 그려서 에러를 '최소화'하는 직선을 구하는 개념이라고 볼 수 있음
MSE(Mean Squared Error)

- Error = ∑Error ^2
- MSE = Error / 전체 데이터 개수
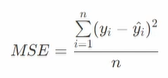
예측 문제는 머신러닝이든 딥러닝이든 MSE 지표를 최소화하는 방향으로 진행하고 평가함
※ 다른 데이터셋의 MSE값과 비교하면 안 됨
같은 데이터셋을 다른 모델로 돌렸을 때의 MSE값끼리 비교해야 함
RMSE(Root Mean Squared Error) & MAE

일반적으로는 MSE를 가장 많이 사용함
회귀(숫자) < - > 분류(범주)
R Square(선형회귀만의 평가 지표)
R Square의 기저 : 평균값보다는 예측을 잘 해야 예측한다

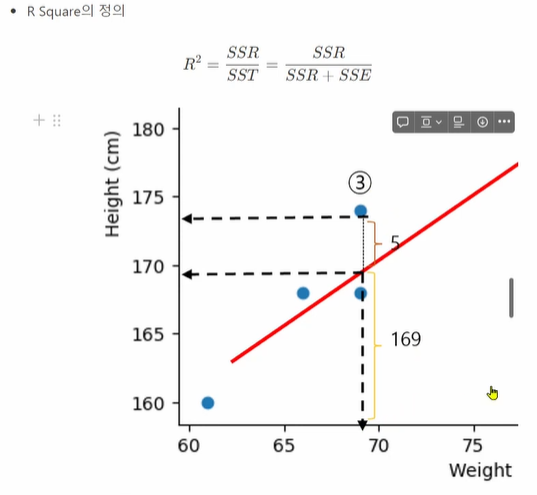
SST : 실제값 - 평균값
SSE : 실제값 - 예측값(작을수록 좋음)
SSR : 예측값 - 평균값(클수록 좋음)
169^2 / 174^2 = 0.94
모델의 특정 값에 대한 설명력 = 94%
독립변수를 여러 개 넣고 싶으면?
→ 다중선형회귀
수치형
1. 연속형
ex) 키 169, 171 사이에는 무수히 많은 수가 있음
2. 이산형
ex) 주사위 4, 6 사이에 존재하는 수가 없음
범주형
1. 순서형
ex) 학점(A, B, C...)은 순서가 있음
2. 명목형
ex) 혈액형(A, B, C)은 순서가 없음
sklearn.linear_model 中 LinearRegression 프로세스
1. 변수에 모델 넣기(model_lr = LinearRegression())
2. 모델 학습(model_lr.fit(독립 변수, 종속 변수))
3. 예측값 확인(model_lr.predict(독립 변수))
4. MSE, R2 Score 확인(sklearn.metrics 中 mean_squared_error, r2_score)
1) MSE
- mean_squared_error(실제값, 예측값)
2) R2 Score
- r2_score(실제값, 예측값)
5. 참고
1) model_lr.coef_ : 가중치
2) model_lr.intercept_ : 편향(y 절편)
'데이터 분석 공부 > 머신러닝' 카테고리의 다른 글
| 머신러닝 심화 복습(데이터 구조, EDA 시각화, 기술 통계, 이상치)(24.05.06) (0) | 2024.05.06 |
|---|---|
| 머신러닝 기초 복습(로지스틱 회귀)(24.05.03) (0) | 2024.05.03 |
| 머신러닝 - 클러스터링(계층적 군집화) (0) | 2024.04.02 |
| 이커머스 머신러닝 강의 복습(Ch.3 - KNN) (2) | 2024.02.28 |
| 이커머스 머신러닝 강의 복습(Ch.2 - Logistic Regression) (0) | 2024.02.27 |



